Binary Bomb Lab - phase 4
Introduction
Phase 4 analysis
Debugging
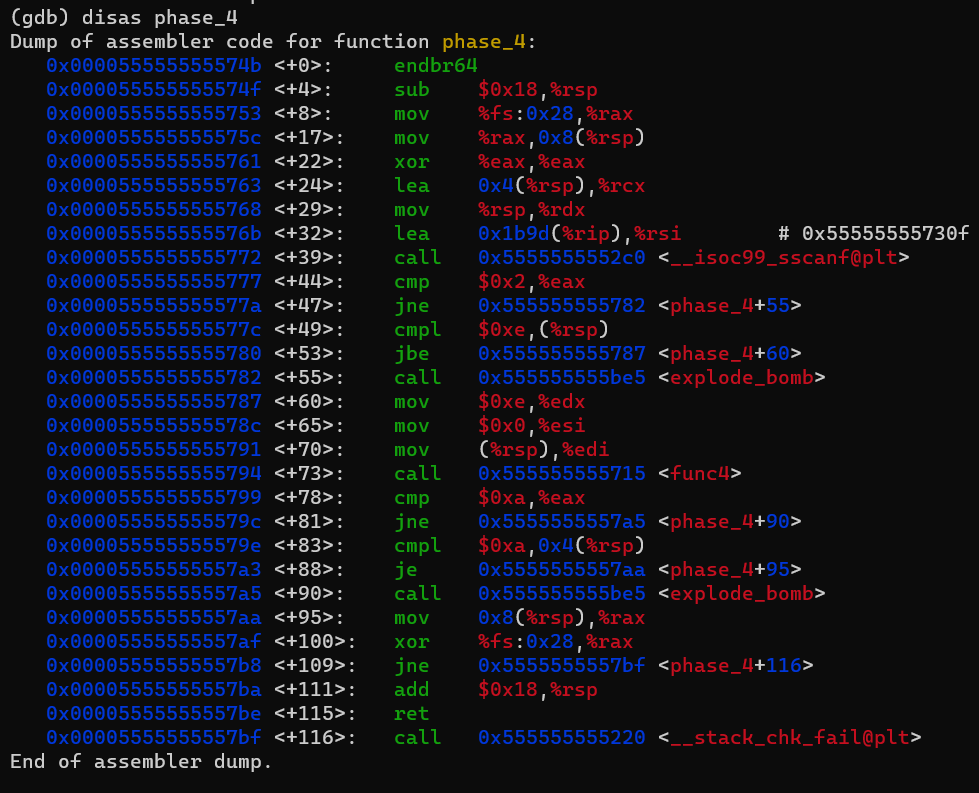
let’s disassemble it :
It starts with the same pattern, check for input format using sscanf, if you examined the format, it stores ; "%d %d" so it needs to integers. and it checks the first value if it less than or equal to 14.
then it calls func4 with three parameters : my first input value, 0, 14. the last 2 parameters seems that it passes to it a specific range. then it checks if the returned value of that function if it equals to 10 and my second input 2. so now we know that my first input should be less than or equals to 14, and my second input should be 10.
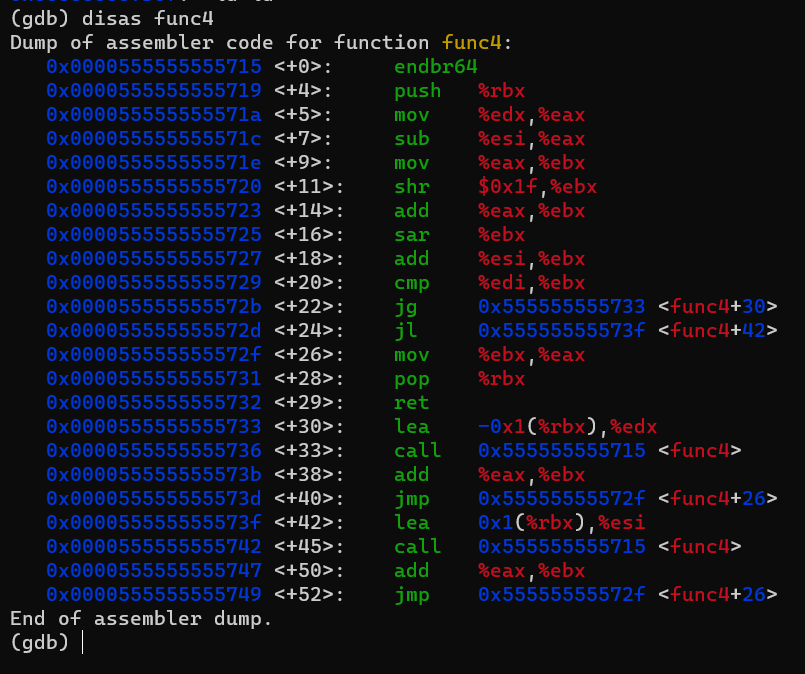
now let’s disassemble the func4 to see what input should it take to return 10.
So here’s the disassemble of it. at first you see some mathematics operations then comparison, and there’s at the end a call to the same function. so it do some recursion. let’s analyze it block by block
0x0000555555555715 <+0>: endbr64
0x0000555555555719 <+4>: push %rbx
0x000055555555571a <+5>: mov %edx,%eax
0x000055555555571c <+7>: sub %esi,%eax
0x000055555555571e <+9>: mov %eax,%ebx
0x0000555555555720 <+11>: shr $0x1f,%ebx
0x0000555555555723 <+14>: add %eax,%ebx
0x0000555555555725 <+16>: sar %ebx
0x0000555555555727 <+18>: add %esi,%ebx
First, this block of code use some trick to do an operation. it first subtract the second and the third parameter then the resulted value will shift it right by 31 bit (0x1f). then it will add the resulted value after shifting and before, and at last it shift arithmetic it right by one byte.
This is actually a trick that the compiler uses to divide a signed value by 2 . because the signed value can be act differently when i want to divide it by two (using sar) when it’s a negative value.
The operation first starts with the subtraction of the second and third parameter as said before. then get that value resulted and try to divide it by half, by first check if it’s a negative or positive value by shifting it right by 31 ( to make only value resides in the register is the last bit which is the sign bit) then add that bit to the original value; so if the original value was positive it will add nothing to it and the divide will continue normally, but if the value was negative it will add one to that original value, this operation can be implement in other ways like:
mov ax,-1
and ax,ax
jns SomePlace ; jump if it positive
add ax,2-1 ; and to it n-1 because it's negative
SomePlace:
sar ax, 1 ; now do the divide
All would work will. then after check if it was negative or not ( the adding one to it will solve the problem of dividing a negative value 2. or division by any integer n, see this for farther read ). then it adds the second argument again to the final result ( at offset <+18>).
If you tracked that math operations it will be like so :
newValue = ((arg3 - arg2 + (arg2 > arg3)) / 2 ) + arg2
// the (arg2 > arg3) just checks if the resulted value is negative or not; to add one or not to the final result. so it resultes 1 when arg2 > arg3, and 0 in opposite case.
which is exact as doing so :
newValue = (arg3 + arg2 + (arg2 > arg3)) / 2
Now we can see that this block of code just try to get the middle value between the second and third element. and depending on the comparison (arg2 > arg3); the final result will always rounds toward the arg2.
Done with this block, let’s take another one :
0x0000555555555729 <+20>: cmp %edi,%ebx
0x000055555555572b <+22>: jg 0x555555555733 <func4+30>
0x000055555555572d <+24>: jl 0x55555555573f <func4+42>
0x000055555555572f <+26>: mov %ebx,%eax
0x0000555555555731 <+28>: pop %rbx
0x0000555555555732 <+29>: ret
0x0000555555555733 <+30>: lea -0x1(%rbx),%edx
0x0000555555555736 <+33>: call 0x555555555715 <func4>
0x000055555555573b <+38>: add %eax,%ebx
0x000055555555573d <+40>: jmp 0x55555555572f <func4+26>
0x000055555555573f <+42>: lea 0x1(%rbx),%esi
0x0000555555555742 <+45>: call 0x555555555715 <func4>
0x0000555555555747 <+50>: add %eax,%ebx
0x0000555555555749 <+52>: jmp 0x55555555572f <func4+26>
It starts with comparison to our final result and the first argument (which is my first input) and if they are the same they will return that value and if not it will go to another call to the same function but with different arguments. so if my input is bigger than the final result it will call the function with arguments : (myInput, finalValue + 1, 14) and if my input is less than the final value it will call it with arguments : (myInput, 0, finalValue +1). you may notice that the first argument is always the same, but the second and the third are changing according to who is bigger. and finally it returns that returned function + my final value. so if you want to write this function in high-level code it would be like :
finalValue = (arg3 + arg2 + (arg2 > arg3)) / 2;
if (finalValue > arg1)
return func4(arg1, arg2, finalValue - 1) + finalValue;
else if (finalValue < arg1)
return func4(arg1, finalValue + 1, arg3) + finalValue;
else
return finalValue;
This is actually the binary search algorithm. that finalValue is actually the mid point between the start and the end of the range (which are the second and third arguments) and check if that inputted value equals to that mid point or not, and according to the result it will return. so if it’s not it will return the returned value from the another call to the same function + the finalValue; so this function actually get the index of the entered value between range 0 - 14 and returns the sum of mid points it hits in every call to it.
so we want make this function returns 10. the first call to that function will always return 7 ( because it’s the first mid point between 0 - 14) so we need to make the second call to the function returns 3 (to make it all returns 3 + 7 = 10).
and if you noticed that the mid point between 0 - 7 is 3. so here we need to enter 3 to it; to make the first call return 7 + another call which will use the lower range between (0-7) and then get the mid point between them which would be 3 and it my input equals to that mid point it will just return it.
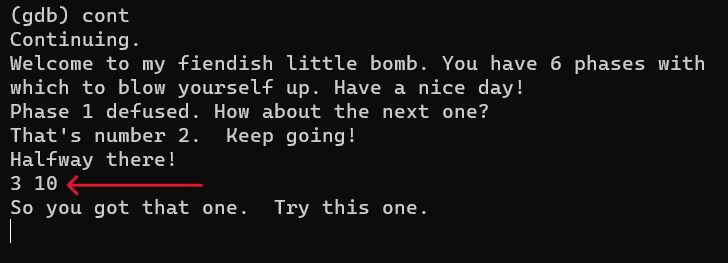
so let’s try my final answer to that phase (3 10):
HERE WE ARE PHASE 5